|
L'ONDE
SONORE
Voyons tout d'abord,
pour bien comprendre, la version théorique simplifiée
d'un signal audio : le son pur.
Son
pur:
Tout d'abord, il
faut savoir qu'un son pur n'existe pas dans
la nature. Il correspondrait à un son d'une
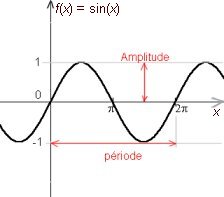
seule fréquence. Il est représenté par le mouvement
vibratoire le plus simple : la sinusoïde. Nous
schématisons ici les mouvements de l'air où
se propage le signal audio. Ce mouvement est
périodique, on nome sa période T, celle-ci s'exprime
en seconde et représente la durée entre deux
crêtes. On entend par crête le point d'amplitude
le plus fort.
 |
On définit le son pur
par la fréquence (F) de cette sinusoïde.
La fréquence est le nombre de période
de la sinusoïde en une seconde. Elle s'exprime
en Hertz.
1 Hz = 1 cycle par seconde.
On nommera couramment un son grâce à sa
fréquence. En musique par exemple la note
référence qui est le " La " et est aussi
nommée " La 440 " car sa fréquence est
de 440 Hz.
|
Autre élément
important, la longueur d'onde. C'est la distance
en mètre entre deux crêtes consécutives, représentée
par le lettre grec lambda. Cette longueur d'onde
permet de comprendre beaucoup sur la propagation
du signal sonore. On la calcule facilement avec
la formule : lambda = C/F
C représente la
célérité (vitesse de propagation du son dans
l'air) C = 340 m/s. Dans un autre milieu que
l'air il faudra remplacer C par la vitesse de
propagation du son dans le milieu étudié. F
est bien sûr la fréquence dont on veut connaître
la longueur d'onde. Cette formule nous permet
de dire que plus la fréquence est basse plus
sa longueur d'onde est importante.
Nous avons vu
les principaux termes et caractéristiques pour
définir notre son pur, maintenant voyons comment
se compose un signal audio plus réel.
Son
complexe:
C'est M Fourier
qui a trouvé en premier comment on pouvait analyser
un signal audio. Il a trouvé que l'on pouvait
exprimer un son périodique comme un son composé
de plusieurs sinusoïdes.
Sur les schémas
suivants proposés (en cliquant sur les
liens correspondants)vous pouvez voir la différence
entre un son
pur et un son
complexe.
Grâce à cette découverte
nous pouvons donc reprendre les paramètres d'une
sinusoïde comme on a vu précédemment et les
appliquer à n'importe quel signal audio car
il sont tous (normalement) périodiques. L'analyse
se fait à partir de la fréquence la plus basse
que l'on nomme fondamentale. Elle donne la hauteur
(grave où aigu) de la note. C'est à partir de
cette fréquence que l'on peut appliquer nos
calculs.
Les autres fréquences,
qui sont donc plus hautes, sont nommées harmoniques.
Elles sont produite par tous ce qui entoure
le signal sonore et qui répond naturellement
au vibrations que ce dernier engendre. Dans
le cas d'un voie humaine les cordes vocales
ne peuvent pas vibrer qu'à une seule fréquence,
elles en produiront naturellement d'autre. Il
y a aussi la résonance de notre corps entier,
les réflexion du lieu ou l'on se trouve et plein
d'autre paramètres qui font qu'une fréquence
seule ne peut pas exister.
Les harmoniques
sont des multiples de la fondamentale.
Ex : f =440 Hz
f1 = 880 Hz (2f)
f2 = 1320 Hz (3f)
f3 = 1760 Hz (4f)
f4 = …
Les harmoniques
donnent le timbre du son. C'est grâce a elles
que l'on peut dissocier les différents instruments
et reconnaître les voix. La forme d'onde des
sons complexes est dite irrégulière.
Suite:
La chaîne acoustique >>
|